fluorF's Laboratory
웹사이트 소개
Introduction of the website
fluorF 소개
Introduction of fluorF
새로운 소식
News
하루 이야기
Daily essay
글
Articles
사진첩
Album
방명록
Guestbook
글
Articles
음악 4
Music 4
음악과 물리학
Music and Physics
피아노 현
Piano Strings
전편에서 피아노가 다른 건반악기로부터 구별되는 가장 큰 특징 중 하나가 해머라고 했었다. 이 해머는 건반이 눌림과 동시에 현을 강하게 타격하고 후퇴함으로써 소리를 만들어내는데, 이번 편에서는 과연 해머가 현을 때리게 될 때, 그리고 때리고 난 뒤 피아노줄에 유도되는 파동의 특성을 이해하고 이를 통해 피아노줄의 특징과 그로 인한 피아노 소리의 특성 등을 이야기하고자 한다. 아, 논의를 시작하기에 앞서서 이 글에서는 피아노줄을 현(絃)이라는 단음절 단어로 간단하게 표현하고자 하니 오해 없기를 바란다.
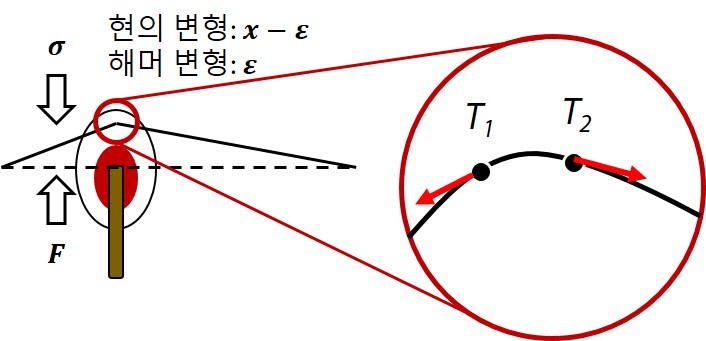
해머가 현을 위로 강하게 때려 올리면 현에 위쪽으로 변형(x-ε)이 생기고, 해머에도 변형(ε)이 생긴다는 것을 전편에서 언급했었다. 그런데 물리학에서 현은 대체로 미소한 단위의 점 성분들이 장력(tension)에 의해 서로 1차원적으로 연결되어 있는 것으로 인식된다. 따라서 아래 그림에서와 같이 변형된 현을 확대해서 살펴본다면, 변형된 부분의 점 성분들은 모두 휘어진 현의 접선의 방향으로 장력을 받게된다고 기술할 수 있다.
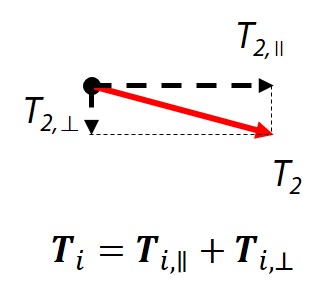
변형된 현에 작용하는 장력들을 모두 더하면 어떻게 될까? 힘은 벡터(vector)이므로 벡터합을 잘 생각해보자. 현이 수평하게 놓여있다는 가정하에서 계산할 때, 우선 장력을 수평방향 장력(T∥)과 수직방향 장력(T⊥)으로 나눠서 생각할 수 있다. 그렇다면 장력의 합은 수평방향 장력들의 합과 수직방향 장력들의 합과 같을 것인데, 다행히도(?) 수평방향 장력의 합은 0이 된다. 그러니 수직방향으로 현을 퉁길 때 현이 왼쪽이나 오른쪽으로 움직이지 않는 것이다. 수직방향 장력들의 힘을 다 합치면 (이상적으로는) -(F-σ)가 된다. 즉, 해머가 현을 변형시킬 때 밀어붙인 힘과 크기는 같으나 반대는 방향인 장력이 변형된 현에 형성되어 해머를 아래 방향으로 짓누르는 것이다. 이것은 뉴턴의 제3법칙인 작용-반작용의 법칙을 이해하면 너무나 쉽게 이해할 수 있는 부분이다.
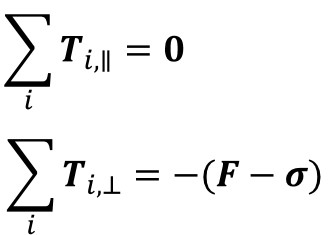
따라서 윗 방향으로 변형된 현에는 아랫 방향으로 작용하는 힘이 생겨 결국 위로 퉁긴 현은 제자리를 지향하는 듯 아래로 향하게 된다. 이처럼 원래 자리로 돌아가고자 하는 힘을 복원력(restoring force)이라고 부르며, 용수철이 왔다갔다하는 것도 이와 같은 복원력 때문이다. 아무튼 이 복원력에 의해 현은 제자리로 돌아가려고 한다. 그러나 뉴턴의 제1법칙이 현을 가만 놔두지 않는다. 바로 관성(慣性, inertia) 때문에 현이 제자리에서 멈추지 못하고 그대로 아래로 더 나아가 휘어지게 되는 것이다.
그러면 현이 아래 방향으로 변형된 것이고 위에서 펼친 논리에 따르면 이제는 복원력이 윗 방향으로 작용하게 된다. 따라서 현은 위로 움직여 원래 자리를 되찾으려고 한다. 하지만, 역시 관성 때문에 현은 제자리를 지나쳐 위로 휘어지게 된다. 현이 에너지를 잃지 않는다면 이 왔다갔다 진동은 무한히 지속될 것인데, 이 운동이 바로 현의 파동이다. 해머가 현을 때리게 되면 현이 진동하게 된다는 사실은 누구나가 잘 알고 있지만 이렇게 물리학적으로 해석할 수 있는 것이다.
그런데 현은 당연하게도 양쪽 끝이 고정되어 있다. 따라서 해머의 타현으로 인해 형성된 파동은 현을 따라 전파되다가 양쪽 끝에서 반사된다. 그리고 이 파동은 이전의 파동과 겹쳐져서 간섭을 일으키고... 가만, 이거 어디서 들어본 내용 아닌가? 바로 2편에서 정상파를 언급할 때 나온 이야기이다. 즉, 해머가 현을 때리게 되면 현에는 정상파가 형성된다는 것이 결론이다.
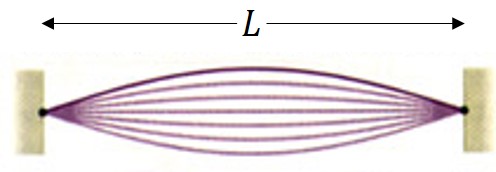
정상파도 파동의 일종이며 파동은 파동의 방정식을 만족시키는 해(解)이다. 1차원 현에 수직 방향으로 진동하는 파동을 역학적으로 계산하면 다음과 같은 미분 방정식의 꼴을 얻을 수 있다.

한편 속도 v로 진행하는 파동은 일반적으로 y(x,t) = A sin[2πf(x-vt)] 와 같은 사인함수로 표현할 수 있으므로 이 식을 위 미분 방정식에 대입하면 다음과 같은 결론을 얻을 수 있다.
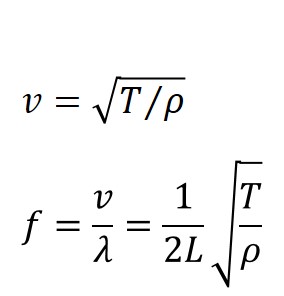
현에 유도된 파동의 속도와 진동수의 표현을 자세히 살펴보면 세 가지 인자가 이들 값에 영향을 주는 것을 알 수 있다.
- L: 현의 길이
- ρ: 현의 선밀도
- T: 현에 걸리는 장력
그리고 각 인자 값이 증가하거나 감소하면 그에 따라 파동의 진동수가 다음과 같이 변하게 되는 것을 알 수 있다.
| 증가 | 감소 | |
|---|---|---|
| L | f ↓ | f ↑ |
| ρ | f ↓ | f ↑ |
| T | f ↑ | f ↓ |
현의 진동수가 소리의 무엇과 관계된 인자였는지 기억이 나지 않는다면 1편을 다시 참고하라. 현의 진동수는 소리의 음높이와 관련된 것이었다. 진동수가 높아질수록 높은음이며 진동수가 낮아질수록 낮은음인 것이다. 따라서 물리학적으로 구한 저 진동수 식에 따르면 피아노의 음정은 현의 길이, 선밀도, 그리고 장력에 의해 제어되어야 할 것이다. 실제로 그럴까? 물론이지. 물리학은 거짓말을 잘 못한다.
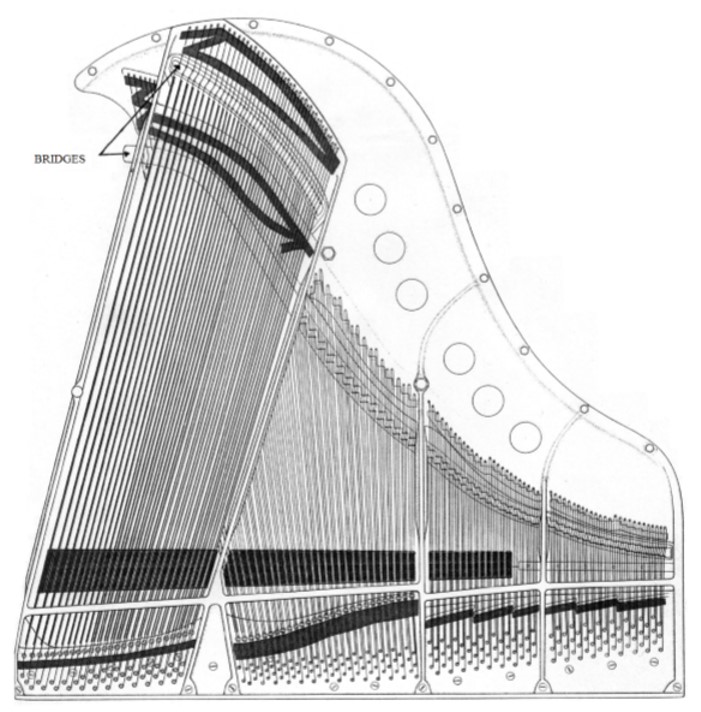
피아노 내부 사진을 다시한 번 기억해보면, 건반이 내는 음높이가 높을수록 현의 길이는 짧아지고 반대로 음높이가 낮을수록 현의 길이가 길어진다. 이것은 정확하게 위에서 살펴본 현의 길이(L)와 진동수(f) 사이 관계에 들어맞으며, 업라이트 피아노든 그랜드 피아노든 이 법칙을 눈으로 직접 확인해볼 수 있다. 특히 그랜드 피아노의 경우 베이스 영억의 건반은 낮은음을 내니까 진동수를 낮추기 위해 현의 길이가 길어져야 하므로 대체로 한쪽이 길게 삐져나와 있는 외형을 갖추게 되는 것이다. 그런데 여기에 문제가 하나 있다. 대체로 가온다(C4)2 음을 내는 건반에 연결된 줄의 길이는 대략 0.62 m 이다. 따라서 현의 길이만으로 진동수를 낮추려고 한다면 일반적인 피아노의 가장 낮은 음(A0)을 내는 건반에는 무려 6 m 길이의 현이 연결되어 있어야만 한다. 6 m 는 너무 길다. 무슨 방법이 없을까? 이럴 때는 L 말고 다른 인자를 제어하면 된다. 바로 선밀도(ρ)이다.
어떻게 하면 현의 선밀도를 높일 수 있을까? 가장 간단한 것은 현의 굵기를 다르게 하는 것이다. 굵은 현은 부피가 크단 뜻이고 동일한 밀도 하에서 큰 부피는 곧 큰 질량을 의미하니 굵은 현은 단위 길이당 질량이 커질 수밖에 없다.
| 음정 | 진동수 (Hz) | 현의 굵기 (mm) |
|---|---|---|
| C8 | 4186 | 0.76 |
| C7 | 2093 | 0.81 |
| C6 | 1047 | 0.86 |
| C5 | 523 | 0.95 |
| A4 | 440 | 0.95 |
| C4 | 262 | 1.00 |
위에서 알 수 있듯이 음높이가 낮아질수록 현의 굵기가 점차 굵어지는 것을 알 수 있다. 그러나 여기에도 한계가 있다. 가장 낮은 음인 A0의 진동수가 28 Hz인데, 이를 만족시키려면 현의 굵기가 3 mm 이상 되어야 할텐데 과연 굵기가 3 mm 이상인 현을 악기 줄이라고 표현할 수 있을까? 그것은 가는 금속 막대기가 될 것이다. 그리고 가는 금속 막대기는 이상적인 현과는 거리가 멀기 때문에3 여기서 생성되는 파동은 앞에서 간단하게 살펴본 방식을 따르지 않게 될 것이며 그 결과 기대했던 음정과는 전혀 다른 엉뚱한 소리가 둔탁하게 날 것이 뻔하다. 따라서 다른 방법이 필요한데, 이를 극복하기 위해 중심현에 또다른 현을 주변에 는 방식이 활용되었다. 기타를 쳐본 사람들은 대번에 알아차릴텐데, 가장 가는 기타줄은 단선이지만, 가장 두꺼운 기타줄은 압축해놓은 용수철마냥 뭔가 칭칭 감겨있는 줄이지 않는가. 피아노줄도 그렇다는 것이다. 즉, 아래 그림에서처럼 다른 줄을 중심현 주변으로 돌돌 감아 피아노줄을 만드는 것이다.

| 음정 | 진동수 (Hz) | 현의 굵기 (mm) | 감은 줄의 굵기 (mm) |
|---|---|---|---|
| A3 | 220 | 1.0 | 0.0 |
| C3 | 131 | 0.9 | 0.3 |
| A2 | 110 | 0.9 | 0.5 |
| C2 | 65 | 1.0 | 1.0 |
| A1 | 55 | 1.1 | 1.0 |
| C1 | 33 | 1.4 | 1.8 |
| A0 | 28 | 1.6 | 2.0 |
표에서도 확인할 수 있듯이 음정이 낮아질 수록 현의 굵기가 조금씩 굵어짐과 동시에 감은 줄의 굵기 역시 굵어지는 것을 알 수 있다. 이렇게 줄을 감으면 중심 현의 거동에 큰 제약을 주지 않은채 선밀도를 효과적으로 늘릴 수 있게 된다. 굳이 예를 들자면, 마른 사람이 두터운 패딩을 입는 것과 마찬 가지이다. 겉에서 보기엔 뚱뚱한 사람과 체형이 비슷하지만 움직임은 패딩 없이 뛰어다닐 때와 큰 차이가 없지 않은가! 아무튼 이렇게 감은 줄을 이용해서 현의 선밀도를 효과적으로 제어한 덕분에 베이스 영역 건반에 연결된 현의 길이가 무작정 길어지는 걱정을 하지 않아도 되었다. 그 결과 연주회용 그랜드 피아노의 사이즈가 3 m 정도를 넘지 않을 수 있게 되었고 외형이 지나치게 길어져 괴상하게 보이는 걱정도 덜 수 있었다.
그렇다면 마지막 다른 인자인 장력은 음높이에 어떻게 영향을 줄까? 장력은 현이 팽팽하게 잡아당겨진 정도라고 볼 수 있는데, 피아노 내부를 잘 들여보면 알 수 있지만 각 현은 모두 양쪽의 핀에 의해 고정되어 있는데, 건반쪽에 있는 핀을 튜닝 핀(tuning pin)이라고 하고, 반대편에 고정되어 있는 핀을 히치 핀(hitch pin)이라고 한다. 그런데 튜닝 핀이라고 이름이 붙은 이유가 뭘까? 이 핀은 나사처럼 되어 있어서 렌치를 이용하여 쉽게 시계 방향 혹은 반시계 방향으로 돌릴 수가 있다. 튜닝 핀에 현이 감겨 있는 형태를 자세히 보면 마치 기타 줄이 매여 있는 튜닝 펙(tuning peg)을 보는 것과 유사하게 돌돌 감겨 있는데, 튜닝 핀을 한쪽 방향으로 돌리면 줄이 더 감기게 되고 반대 방향으로 돌리면 줄이 풀리게 된다. 줄이 더 감기게 되면 핀 사이에 있는 줄은 더 팽팽하게 잡아당겨지므로 현에 인가된 장력은 증가하게 된다. 따라서 현에 유도된 정상파의 진동수가 증가하게 된다. 바로 이러한 방식으로 장력이 피아노 음높이에 영향을 주는 것이다.
장력을 이용한 음높이 조절은 대개 피아노 조율사가 집이나 연주회장을 방문했을 때 확인할 수 있다. 조율사는 손상된 현을 교체하고 해머 구조의 이상을 점검함과 동시에 렌치를 이용하여 튜닝 핀을 조였다 풂으로써 원래 내야 하는 소리를 벗어난 건반 소리를 바로 잡는데, 이 과정이 곧 장력을 제어하여 음정을 맞추는 것이다.
골드베르크 변주곡 아리아와 1번 곡이 끝난 뒤인 3분 59초부터 조율사가 등장한다.
그런데 우리는 음높이를 결정 짓는 현의 진동수에만 관심있는 것이 아니다. 어떻게 보면 더 중요한 것은, 피아노는 어째서 피아노 소리를 내는가, 곧 어떠한 이유로 피아노는 해당 진동수의 음을 그런 음색으로 내는가 하는 것에 있다. 반복해서 말하지만 소리의 맵시는 파형과 관련이 있다. 따라서 이제는 피아노에 형성되는 파동의 형태를 분석할 차례이다.
역시 지속적으로 반복하여 이야기했지만, 해머가 현을 때리게 되면 초기 현에는 수많은 진동이 형성되지만 정상파를 제외한 다른 파동들은 재빠르게 상쇄 간섭으로 인해 소멸된다. 결국 오랫동안 현에 남아서 우리 귀에까지 전달되는 소리의 진동을 야기하는 파동은 정상파 뿐이다. 그런데 현에 형성되는 정상파는 모두 몇 개일까?
아니 무슨 소리를 하는 것인가? 아까 얘기하지 않았나? 아래와 같은 정상파가 생긴다며?

독자들에게 사과를 해야할 것 같다. 사실 현에 형성되는 정상파는 이것뿐만이 아니다.
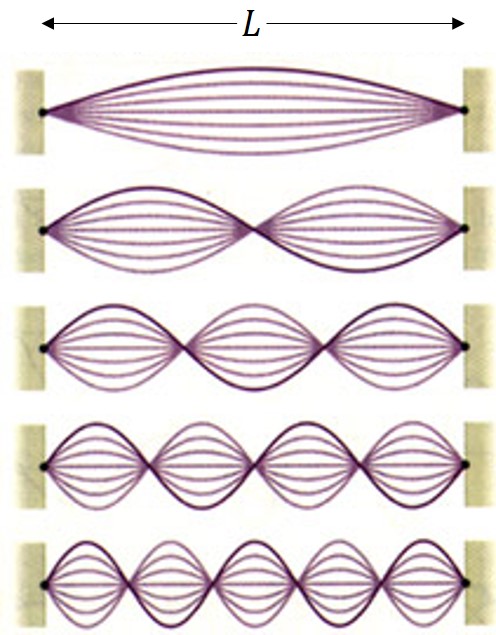
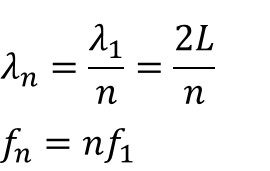
이론적으로는 이와 같이 무수한 개수의 정상파가 형성된다. 처음에 보여주었던 기본 정상파를 기음(fundamental) 혹은 1차 배음(first harmonic)라고 부르는데 이 정상파의 파장은 2L이 된다. 그 아래 정상파를 보자. 우리는 이것을 2차 배음(second harmonic)이라고 부를 수 있는데, 이 정상파의 파장은 L이 된다. 그 아래는? 3차 배음(third harmonic)의 파장은 2/3 L이다. 이와 같이 일반화를 하면 n차 배음의 파장은 2L/n이라고 쓸 수 있다. 즉, 정상파의 배음 차수가 늘어날수록 파장은 2배, 3배, 4배... 작아진다. 그런데 이 정상파들은 모두 같은 매질에서 같은 힘을 받아 같은 속도로 움직이는 파동들이다. 파동의 속도는 진동수와 파장의 곱으로 나타낼 수 있으므로 (v=fλ), v가 같은 값을 유지하려면 배음 차수가 늘어날수록 진동수는 오히려 2배, 3배, 4배... 커져야 한다.
그러니 이 말은 무엇을 뜻하는가? 우리가 현 하나를 진동시키면 그 안에는 우리가 기대했던 진동수를 가지는 정상파(기음에 해당) 뿐만 아니라 그 진동수의 정수배를 가지는 수많은 높은음들(배음에 해당)이 동시에 한 소리로 울려퍼진다는 것을 뜻한다. 거짓말! 그런데 어째서 우리는 헛갈리지 않고 그 피아노 건반 소리를 하나의 음으로 인식하냔 말이다.
이를 이해하려면 조금 복잡한 역학 지식이 동원된다. 일반적으로 기술되는 현의 진동은 여러 정상파들의 선형 조합(linear combination)으로 기술될 수 있다고 2편에서 잠깐 언급한 적이 있었다. 선형 조합이란 간단히 말해서 어떤 파동을 기술할 때 그 구성요소들에 적당한 계수를 곱한 뒤 더한 꼴로 나타낼 수 있다는 것을 의미하며 수식으로 y(t)=Σaixi(t) 와 같이 나타낼 수 있다는 것이다. 이 때 계수들이 모두 다른데 계수는 파동의 진폭, 곧 소리 크기와 관련된 수치라는 것을 또한 2편에서 얘기한 적이 있었다. 피아노 현에서 발생하는 파동은 엄청나게 복잡미묘하지만 초기 조건과 경계 조건들이 주어진다면 각 정상파들의 계수는 이론적으로 계산할 수 있다. 4 그런데 진동을 제어하는 다른 상황 ㅡ 예를 들면 현에 손을 갖다댄다든지 ㅡ 만 없다면, 대체로 배음의 계수는 기음의 계수보다 낮다. 그런데 파동의 에너지는 진폭의 제곱에 비례하기 때문에 배음의 에너지는 기음의 에너지에 비해 훨씬 낮아지게 된다. 따라서 기음의 소리가 가장 크게 들리는 것이다. 게다가 소리가 천년만년 지속될 것이 아닌이상 시간이 지나면 소리 에너지는 감쇄될 것이므로 높은 차수의 배음은 거의 들리지 않을 정도가 될 것이며 가장 큰 에너지를 지녔던 기음의 소리가 가장 늦게까지 악기 소리를 지배할 것이다. 그러니 피아노 건반 하나를 눌렀을 때 수많은 음이 발생한다고 해서 걱정할 필요는 전혀 없다.
그래도 못 믿겠다고? 예를 들어 어떤 악기가 C5 음을 낸다고 생각해보자. 기음의 파동만을 가지고 C5 음을 내면 다음과 같은 소리가 나온다.
텔레비전 조정 시간에 등장할 것 같은 전자음으로 이 파동의 파형은 순수한 사인(sine) 곡선이다. 만약 피아노 건반을 눌렀을 때 기음의 파동만이 등장하고 다른 정상파들이 등장하지 않는다면 저런 소리가 들려야 한다. 정말 그렇게 생각하나? 애석하게도(?) 실제 피아노 음의 파형은 다음과 같다.
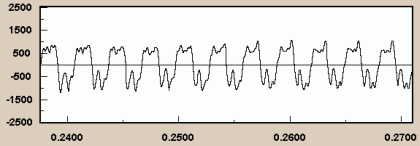
이것이 의미하는 것이 무엇인가? 이 파동의 진동수는 C5 음에 해당하는 523.25 Hz가 맞지만, 파동의 파형은 단순한 사인 파동의 그것이 아니며 꽤나 복잡 미묘하게 생겼다. 그런데 이 복잡 미묘하게 생긴 원인이 바로 무엇이냐 하면 바로 이 기음의 배음들, 즉 진동수가 1046 Hz, 1569 Hz 등등인 정상파들이 서로 더해졌기 때문이다. 2편에 등장했던 그림 하나를 다시 끄집어내면 이해가 빠를 것이다.
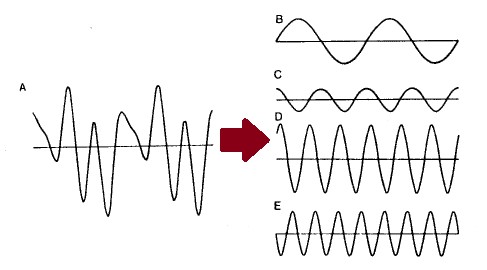
즉, 현에 발생하는 모든 정상파는 위의 그림과 같이 기본 정상파들의 선형 조합으로 구성되어 있으므로 곱하기와 더하기를 잘하면 주어진 정상파를 모두 분해하여 이 음이 어떤 배음들로 얼마만큼 구성되어 있는지 계산해낼 수 있을 것이다. 수학자들은 이런 과정을 곱셈과 덧셈을 이용해서 하지 않고 바로 푸리에 변환(Fourier transformation)이라는 기술을 사용하여 해낸다. 푸리에 변환은 시간 도메인의 어떤 함수를 진동수 도메인의 함수로 변환시키는 기법인데, 이를 이용하여 오실로스코프(oscilloscope)에 나타난 파형을 분석하여 어떠한 배음들이 조합되어 있는지 그 계수까지 다 밝혀내 준다.6
그러므로 피아노가 피아노 소리를 내는 이유는 해머가 타현할 때 현에 형성된 정상파가 사실 여러 정상파들의 선형 조합으로 구성된, 매우 복잡한 파형을 파동이기 때문이다. 그리고 그 여러 정상파들의 정체는 기음과 그 기음의 진동수의 정수배가 되는 배음들이란 사실을 꼭 기억해야겠다. (다음 편에 이 이야기가 다시 등장할 것이다.)
해머가 현을 때릴 때 우리는 현이 x만큼 변형된다고 말해 왔었다. 이 변형은 결국 휘어짐(bending)이며 x는 결국 휘어짐에 의한 변위(displacement)가 될텐데, 이를 좀 더 구체적으로 계산하면 다음과 같이 표현할 수 있다.

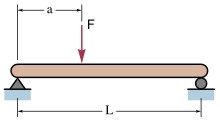
그런데 현이 너무 많이 휘게 되면 장시간의 연주를 버티지 못하고 파괴될 것이다. 따라서 오랫동안 악기를 유지하며 연주하려면 x 값이 작게 유지가 되어야 하므로, 현의 재료는 영의 계수가 높은 물질이어야 할 것이다. 피아노의 발명이 가능하게 된 것도 바로 영의 계수가 높은 물질 기반의 현을 만드는 야금술(冶金術, metallurgy)이 비약적으로 발전했기 떄문이었다. 과거 하프시코드 현은 황동으로 만들어졌지만, 당시 피아노 현은 황동에 비해 강도가 굉장히 좋은 철로 만들어졌는데 현대의 강철 피아노 현은 촬영 시 스턴트맨이 몸을 지탱할 때 쓰일 정도로 매우 강도가 높다. 따라서 기계적 안정성의 측면에서 피아노 현의 높은 인장 강도(tensile strength)는 매우 바람직하다. 그런데 소리의 측면에서는 바람직하지 못한 결과를 낳는다.
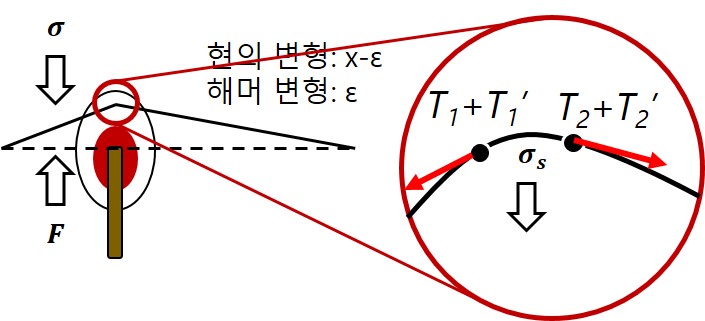
- 현이 휘어진다는 것은, 현의 길이가 변형시 잠깐 길어졌다는 것을 의미한다. 그렇다면 휘어졌을 때 현 내부에서는 현이 짧아지는 방향, 곧 수평 방향으로 추가적인 장력(T1', T2')이 인가될 것이다. 기음의 정상파에서는 추가적인 장력의 영향이 미미하지만, 배음에서는 변형이 훨씬 더 광범위하게 일어나야 하므로 추가적인 장력의 영향이 점차 커질 것이다.
- 이렇게도 설명할 수 있다. 현이 변형되었을 때 우리는 현이 제자리로 돌아가려는 복원력을 받는다고 했었다. 그런데 이상적인 현에서 벗어나 영의 계수가 높은 이런 현의 경우, 해머가 쳐 들어올리는 현상 때문에 발생한 변형 뿐만 아니라 휘어지는 것에 의한 재료 내부의 변형을 고려해야 한다. 왜냐하면 그 변형에 의해 현 내부에 생성되는 응력의 크기가 영의 계수가 높기 때문에 무시 못할 정도로 크기 때문이다. (σ=εE) 그러면 영의 계수를 고려하지 않았던 현과는 달리 영의 계수가 높은 현의 경우 기존의 복원력 F에 추가적인 응력 σs가 추가로 인가된다. 그 결과 복원력의 크기가 커져서 현은 더욱 빠른 속도로 진동하게 된다. 이 추가적인 응력의 크기는 배음의 차수가 커질수록 더 커지기 때문에 기음 진동보다 배음 진동의 속도가 더 빨라지게 된다.
그런데 위의 두 이야기는 같은 얘기다. 앞 장의 논의에서 우리는 이미 장력(T)이 커지면 속도(v)가 커지는 것을 알고 있지 않은가? 결국 두 이야기는 같은 현상의 다른 접근일 뿐 같은 결론을 제시하는데. 바로 배음 차수가 높아질수록 정상파에 걸리는 장력이 커진다 = 정상파의 속도가 빨라진다는 것이다. 그런데 장력이 커지면 정상파의 진동수가 높아지지 않는가? 따라서 우리는 배음 차수가 높아질수록 기존에 예상되었던 기음 진동수의 정수배 값에서 벗어난, 예상치보다 더 커진 값을 갖게 된다는 결론에 이른다.
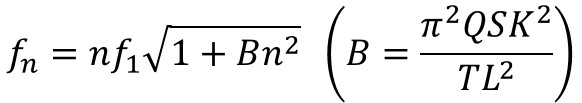
따라서 이 배음들은 더 이상 엄밀한 의미에서는 조화 배음(harmonic overtone)이 아니다. 왜냐하면 진동수 값들이 정확하게 기음 진동수의 정수배가 아니기 때문이다. 이처럼 완벽한 정수배에서 약간 벗어난 진동수를 가지는 파동들을 일컬어 불협화성(inharmonicity)을 갖는다고 하며7 이러한 부조화성을 가진 이들을 부분 배음(partial)이라고 부른다.
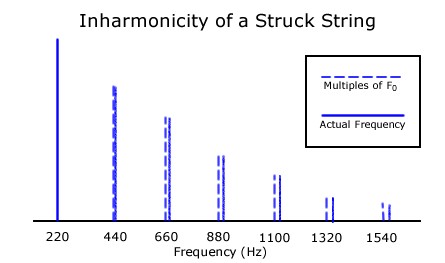
부분 배음의 진동수와 배음의 진동수 사이의 편차인 불협화도가 너무 커지게 되면 현의 소리는 굉장이 둔탁하고 부조화하게 들릴 것이다. 따라서 메이저 피아노 회사들은 피아노 현과 해머 및 전체적인 구조를 굉장히 정밀하게 제어하여 이 불협화도를 최소화하는 데 많은 공을 들였다. 그 결과 부분 배음의 불협화도를 인간이 인지하는 수준 이내에서 제어하는 데 성공하였고, 그 결과 우리는 다행히 조율이 필요한 시점에 이르기 전까지는 이와 같은 부분 배음에 의한 불편을 거의 못 느끼게 되었다.
본편의 내용을 한 문장으로 요약하면 "해머가 현을 때리면 기음과 그의 부분 배음들의 선형 조합으로 구성된 정상파가 발생한다."라는 언뜻 보면 굉장히 단순한 것이다. 하지만 이 결론을 이해하기 위해 이토록 많은 물리학적 고찰이 필요했던 것이다.
- 1피아노 한 대에 피아노줄은 총 몇 개일까? 건반이 88개라서 줄도 88개일 것 같지만 정답은 230개. 베이스 영역의 건반에는 건반 하나당 줄이 하나씩 연결되어 있지만, 나머지 건반에는 건반 하나당 줄이 세 개씩 걸려 있다.
- 2앞의 알파벳 C는 음이름을 나타내는 것이며 뒤의 숫자 4는 옥타브 위치를 말하는 것이다. 앞으로 편의상 음정은 이와 같은 방식으로 표현하고자 한다.
- 3현과 막대기는 소위 강성(剛性, stiffness)에서 차이가 난다. 막대기는 강성이 높은데 이 말은 변형이 잘 되지 않는다는 것을 의미한다. 똑같은 현이므로 영의 계수는 같지만 이렇게 서로 다른 거동을 보이는 것은 재료의 구조, 여기서는 굵기가 다르기 때문이다. 강성은 재료의 종류뿐 아니라 구조에도 영향을 받는 물리량이다.
- 4본 홈페이지의 글 '배음의 물리학'에서 이를 논한 바 있다. https://fluorf.net/xe/?mid=my_words&page=4&document_srl=3833
- 5https://musicscribekit.sourceforge.net/
- 6그렇다면 반대의 과정도 가능할 것이다. 기본 사인 파형들을 발생시키는 장치를 여러 개 연결해서 서로 간섭을 시켜주면 새로운 형태의 복잡 미묘한 파형을 가진 파동을 '제조'할 수 있을 것이다. 바로 이것이 신디사이저(synthesizer)이다.
- 7고전 역학에서 논하는 조화 진동자(harmonic oscillator)의 거동에서 벗어난 정도를 말하는 비조화성(anharmonicity)과는 다르므로 헛갈려서는 안 되겠다.
▲[이전글] 3. 피아노 해머 (Piano Hammers)
▼[다음글] 5. 피타고라스 음률 (Pythagorean Tuning)
 |
이 저작물은 크리에이티브 커먼즈 저작자표시-비영리-동일조건변경허락 4.0 국제 라이선스에 따라 이용할 수 있습니다. |