fluorF's Laboratory
웹사이트 소개
Introduction of the website
fluorF 소개
Introduction of fluorF
새로운 소식
News
하루 이야기
Daily essay
글
Articles
사진첩
Album
방명록
Guestbook
글
Articles
음악 6
Music 6
음악과 물리학
Music and Physics
평균율과 불협화음
Equal Temperament and Dissonance
피아노로 서로 다른 두 음을 쳤을 때 어떤 조합은 '어울린다'는 느낌을 주는 반면, 어떤 조합은 '영 안 어울린다'는 느낌을 주고, 또 어떤 조합은 '묘하게 어울리네'라는 느낌이 있는가 하면, 어떤 조합은 '귀에 거슬린다'는 감정을 선사할 때가 있다. 도대체 이것은 어디에서 기인하는 것일까?
피타고라스 학파의 설명은 다음과 같았다: 두 음의 진동수 비율이 낮은 숫자의 간단한 정수비를 가지면 협화음(協和音, consonance)이고, 높고 복잡한 정수비를 가지면 불협화음(不協和音, dissonance)이다! 예를 들어 옥타브의 경우 두 음의 진동수 비율은 1:2이다. 숫자가 낮은 간단한 정수비니까 이는 협화음정이다. 그러나 C음과 D음을 생각해보면 진동수 비율은 8:9이다. 훨씬 더 숫자가 높아지지 않았나. 그러므로 이것은 불협화음정이다. E음과 F음은 무려 243:256이다. 이것은 대단히 거술리는 불협화음정이라는 결론에 이른다. 놀랍게도 피타고라스의 설명은 굉장히 잘 들어맞는 것처럼 보였다. 이러한 법칙에 근거하여 고대 그리스 시대에서부터 중세 시대에 이르기까지 제주, 완전4도, 완전5도, 옥타브는 협화음정으로 인식되어 화성을 쌓는 기초가 된 반면, 그 외의 음정은 모두 불협화음정으로 간주되었다.
그런데 르네상스 시대를 거치면서 서양 음악에 일대 변혁이 일어난다. 교회의 가르침인 그레고리오 8선법에서 조금 자유로워진 음악가들은 점차 세속적인, 당시로서는 파격적인 새로운 음악 세계를 창조해나가기 시작했는데 이를 아르스 노바(Ars Nova)라고도 한다. 이 아르스 노바 시기 이후 영국, 프랑스, 이탈리아, 네덜란드 등지에서는 기존의 교회 음악에서 탈피한 새로운 양식의 음악들이 쏟아져 나오기 시작했는데 그 중 15세기에 가장 괄목할만한 활동을 보인 작곡가들은 주로 프랑스 속령인 부르고뉴(Bourgogne) 공국(公國)에서 활동했으며 흔히 이들을 일컬어 부르고뉴 악파(Burgundian school)라고도 한다. 그 중 한 사람인 기욤 뒤파이(Guillaume DuFay)의 「Ave Maris Stella」를 한 번 들어보자.
선창이 끝난 뒤 합창이 시작되면 그레고리오 성가와는 전혀 다른 느낌을 주는 것을 확연히 느낄 수 있다. 악보상 보이는 가장 큰 차이는 성부가 소프라노와 테너, 베이스로 확실하게 나눠져 있다는 것인데 여기까지는 성부가 하나 더 늘어난 호모포니의 변형처럼 보인다. 그러나 음정 측면에서 획기적인 차이가 있는데, 각 성부의 음정 간격이 완전 4도나 완전 5도에만 국한되어 있지 않을뿐더러 6도와 3도가 아주 빈번하게 쓰인다는 것이다. 악보를 보면 특히 소프라노 파트와 베이스 파트 사이에 이러한 음정 간격이 자주 나타나는 것을 알 수 있다. 피타고라스 음률을 따르던 당시로서는 불협화음정을 빈번하게 사용한 것이었다. 그런데 이 곡을 듣는 당신, 과연 불협화음정을 자주 느끼며 당혹스러워 했는가 아니면 오 그레고리오 성가보다는 훨씬 더 듣기 좋네 이렇게 생각했는가.
이번에는 같은 시기 활약한 또다른 유명한 작곡가 질 드 뱅슈아(Gilles de Binchois)의 「Adieu, adieu, mon joileux souvenir」을 들어보자.
이 곡의 악보를 잘 살펴보면 B♭ 장음계가 주로 사용되는 것임을 쉽게 확인할 수 있다. 장음계는 아이오니안 모드와 같다고 5편에서 얘기한 바 있지만, 당시 아이오니안 모드는 그레고리오 8선법에 포함되지 않았었다.1 물론 하이포리디안 모드가 아이오니안 모드와 음계 구성이 동일하긴 하지만 그것은 어디까지나 변격 선법으로서의 하이포리디안 모드였을 뿐 당시에는 아이오니안 모드와 같은 음계가 개별적인 어떠한 정격 선법으로서 인식되지 않았다.
여기서 우리는 르네상스 시기 서양 음악의 가장 큰 변화를 파악할 수 있게 된다. 중세 시대의 교회 선법 중심의 음악은 르네상스 시기 이후 세속적인 조성(調性) 중심의 음악으로 옮겨 가게 되었고, 이 과정에서 가장 중요하게 떠오른 음계가 바로 아이오니안 모드에 해당하는 장음계, 그리고 에이올리안 모드에 해당하는 단음계였다. 그런데 이 두 음계의 성격을 명확하게 구별지어주는 가장 중요한 음정 간격은 지금까지 알려진 협화음정인 1, 4, 5, 8도가 아닌 불협화음정인 3도와 6도였던 것이다.
참고로 인류가 왜 장음계를 기쁘고 음계로, 단음계를 슬픈 음계로 인식하게 되었는지 그 이유는 잘 모른다. 어쩌면 우리는 은연중에 그렇게 세뇌된 것인지도 모른다. 하지만 어린 아이들도 '학교 종' 노래를 원래대로 쳐 주면 즐겁게 따라 부를테지만 E와 A음을 죄다 E♭과 A♭음으로 바꿔버리면 어리둥절해하며 '무서워요...'라고 말할 것 같은 표정을 지을 것이다.
문제는 바로 그 중요하디 중요한 3도와 6도 음정 간격이 피타고라스 음률에서는 불협화음정으로 처리된다는 것에 있었다. 아니, 이렇게 듣기 좋은 음정 간격이 어째서 불협화음정이란 말인가! 당시 뒤파이와 뱅슈아를 찬양했던 마르탱 르 프랑(Martin Le Franc)이라는 사람은 책에서 이렇게 그들에게 찬사를 보내기도 했는데 말이다.
...Et ont prins de la contenance Angloise et ensuy Dunstable, Pour quoy merveilleuse plaisance rend leur chant joyeux et notable.
그리고 그들은 영국의 형식을 차용하고 던스터블2을 따랐기에 그들의 노래는 경이적으로 기분이 좋고, 주목할 만한 기쁜 노래가 되었다.
그렇다면 어떻게 해야 하나? 당연히 고칠 것은 고쳐야 하지 않겠는가. 그렇다고 처음부터 완전히 모든 걸 싹 다 뜯어고칠 수는 없는 노릇이었다. 워낙 피타고라스 음률이 고대에서부터 중세까지 서양 음악에 끼친 영향이 컸으니... 그래서 르네상스 시기의 음악가들은 파타고라스 음률을 3도 음정 간격에 대해서만 약간 손볼 수 없나 방법을 찾기 시작했다. 예를 들어 아이오니안 모드에서 C음과 E음을 생각해보자. 피타고라스 음률에 따르면 둘 사이의 진동수 비율은 64:81이다. 이것을 어떻게 하면 아주 조금만 조절함으로써 가장 간단한 비율로 만들 수 있을까? 산수가 빠른 사람이라면 눈치 챘을 수 있겠지만, 81을 80으로 아주 조금만 줄여주면 64:80 = 4:5 가 되는 마법을 경험할 수 있다! 그런데 마법은 여기서 그치지 않는다. C, E, G음을 함께 생각해 보는 것이다. 초등학교 때 배운 연비(連比)를 사용해서 이 세음 사이의 진동수 비율을 구해보면, 피타고라스 음률에서는 64:81:96이 된다. 그런데 아까 81을 80으로 약간 줄이지 않았나. 그러면 64:80:96 = 4:5:6이 되는 연속적인 마법을 경험할 수 있다! 즉, E음을 조금만 내리면 C음과도 잘 어울리고(4:5) G음과도 잘 어울리는(5:6) 음이 될 수 있는 것이다. 여기서 중요한 사실은 C음과 E음, 그리고 E음과 G음은 모두 3도 차이인데 진동수 비율은 동일하지가 않다. 같은 3도임에도 C음과 E음 사이의 간격이 E음과 G음 사이의 간격보다 더 길다. 이런 이유로 C음과 E음 사이의 3도는 메이저(major)로 불리고 E음과 G음 사이의 3도는 마이너(minor)로 불리게 되었다. 우리말로는 각각 장3도, 단3도로 부른다.3 당시 음악가들은 이렇게 E음을 아주 조금 낮춰 조절하면 C 장음계로서의 조성이 명확하게 드러나고 악기의 울림이 굉장히 깔끔해진다는 것을 깨달았다. 이 아주 조그만 차이인 진동수 비율 80/81을 신토닉 콤마(syntonic comma)라고 부르며 고대 그리스 음악가인 디두모스(Δίδυμος)의 이름을 따서 디디모스의 콤마라고도 부른다.4
그런데 3도가 조정되면서 대칭적인 위치에 있던 6도도 수정이 될 수밖에 없었다. 신토닉 콤마를 해결하기 위해 80/81 비율을 적용하면 C, E, C'음 사이의 진동수 비율은 4:5:8이 된다. 마찬가지 이유로 E, G, E'음 사이의 진동수 비율은 5:6:10이 된다. 그 결과 E음과 C'음, G음과 E'음은 같은 6도 이지만 진동수 비율이 각각 5:8 및 3:5가 된다. 이번에는 후자의 음정 간격이 더 길어졌다. 그런데 사실 당연한 것이, 옥타브 진동수 비율은 1:2로 고정이 되어 있기 때문에 3도의 길이가 길어지면 상대적으로 6도의 길이는 짧아지는 것이고, 반대로 3도의 길이가 짧아지면 상대적으로 6도의 길이는 길어지게 되는 것이다. 이런 이유로 전자를 단6도, 후자를 장6도라고 부르게 되었다.
이렇게 신토닉 콤마를 해결함으로써 피타고라스 음률은 다음과 같은 기준을 두고 대대적인 수정에 들어가게 된다. 피타고라스 음률에서는 5도씩 돌아가면서 음정을 맞췄지만, 여기서부턴 앞서 설명한 신토닉 콤마를 고려하여 3도도 함께 바꾸게 되었다.
- 우선 옥타브(C-C') 진동수 비율은 1:2로 고정된다.
- 완전5도(C-G) 역시 진동수 비율은 2:3으로 고정된다.
- 완전4도(C-F) 역시 진동수 비율은 3:4로 고정된다.
- 장3도(C-E) 진동수 비율이 이제는 4:5로 고정된다.
- 단3도(E-G) 진동수 비율이 이제는 5:6로 고정된다.
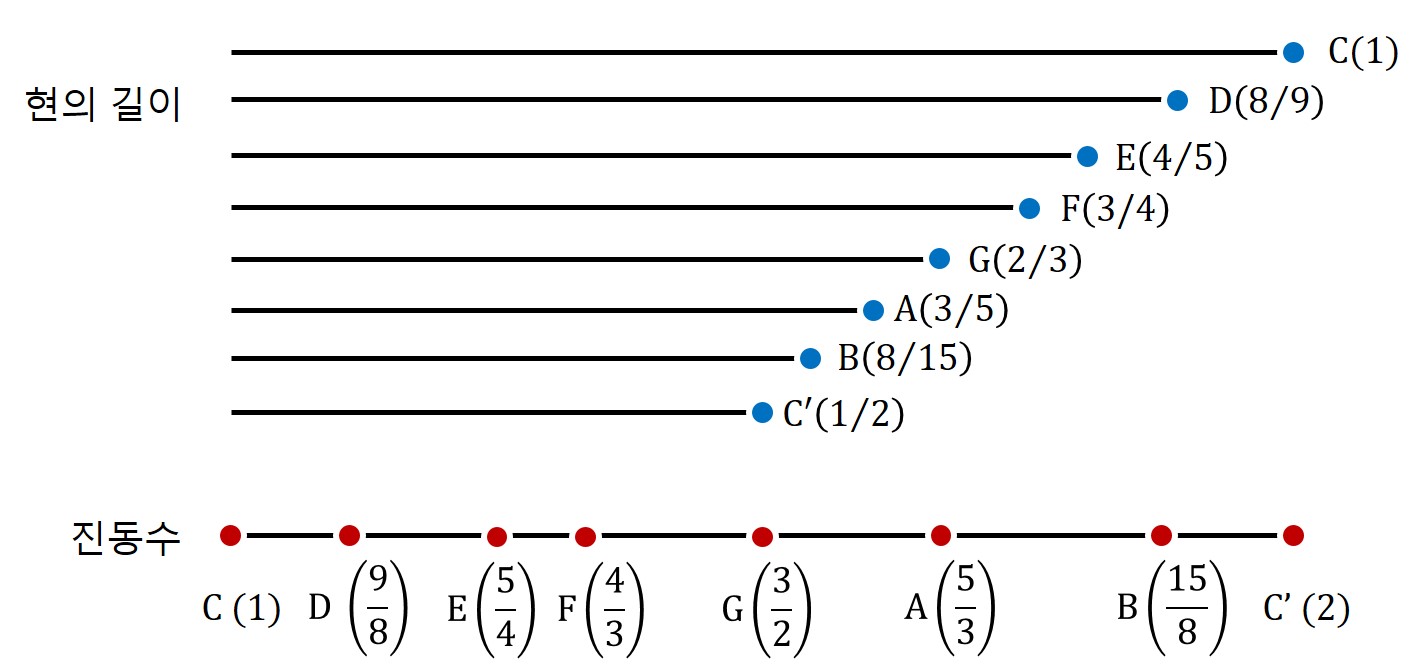
그런데 위의 조건들을 보면 1:2, 2:3, 3:4, 4:5, 5:6 이런 숫자를 보이는 것이 여간 희한한 것이 아니다. 신토닉 콤마를 해결한 것이 정말 우연한 산수 계산에서 비롯된 발견이었을까? 우리는 지난 4편에서 현에 정상파가 형성되면 수많은 배음들이 발생한다는 것을 살펴보았고, 정상파들의 진동수는 모두 기음 진동수의 정수배임을 확인했었다.
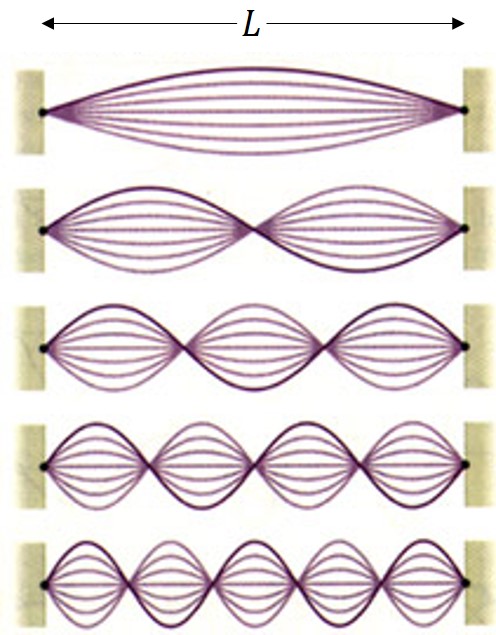
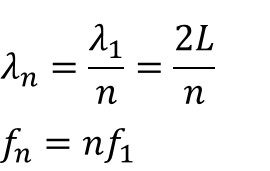
여기서 아주 재미있는 것을 하나 발견할 수 있다. 예를 들어 저 정상파의 기음에 해당하는 파동이 내는 음을 C음이라고 가정하자.
- 그렇다면 1차 배음의 음은 무엇일까? 진동수가 2배니까 C'음이 된다.
- 자, 2차 배음의 음은 어떻게 될까? 진동수가 3배인데, 3=2×(3/2)이므로 C'음에서 완전 5도 올라간 G'음이 될 것이다.
- 오호? 그렇다면 3차 배음의 음은? 진동수가 4배라는 것은 C음에 대해서 두 옥타브 올라간 C''음이 되겠지. 그런데 다시 생각해보니 4=3×(4/3)이므로 아까 음인 G'음에서 완전 4도 올라간 음이어야 하는데 그건 C''음이 맞다.
- 계속 가보자. 4차 배음의 음은? 5=4×(5/4)이므로 아까 음인 C''음에서 장3도 올라간 음이어야 한다. 그것은 E''음이다.
- 기왕 이렇게 된 거 더 가보자. 5차 배음의 음은? 6=5×(6/5)이므로 아까 음인 E''음에서 단3도 올라간 G''음이다.
재미있게도, C음을 연주할 때 거기에 섞여서 나오는 첫 다섯 배음들은 C', G', C'', E'', G''음이 된다. 피타고라스의 논리에 따르면 낮은 차수의 배음들은 기음과 진동수 비율이 1:2, 1:3, 1:4, 1:5 정도로 낮은 숫자로 구성된 간단하 정수비이므로 당연히 기음과 잘 어울리는 음이 될 수밖에 없다. 본래 피타고라스 음률에서의 E''음은 C음과 완전히 불협화인 음정이었지만 신토닉 콤마를 해결하기 위해 E음을 내는 현의 길이를 약간 조절하는 조치를 취하게 되면 E음이 C음의 배음에 속하는, 그래서 꽤 잘 어울리는 음으로 조절이 된다. 즉, E현의 길이를 약간 줄이는 것은 마치 땜질식 시도같이 보여지지만, 기존 C음과 굉장히 잘 어울리는 E음을 파동을 고려한 물리학으로 찾아낸 것과 같은 효과를 보이는 것이다.
이와 같은 방식으로 음정을 맞추는 조율법을 순정률(純正律, just intonation)이라고 한다. 순정률의 핵심은 모든 음들 사이의 비율이 간단한 정수비가 되게 하는 것이며 (결과론적으로는) 이를 위해 정상파의 배음 사이의 진동수 비율(n:n+1)을 음정 간격으로 채택한 것이다. 비록 출발은 3도를 어울리게 조절하는 시도였지만 결론은 물리학적인 고찰에 아주 잘 부합하는 조율법이 된 것이다.
순정률 덕분에 3도 음정 간격은 진동수 비율 4:5 혹은 5:6을 가지게 되어 피타고라스 음률 시대에 나붙었던 64:81이라는 '지저분한 불협화음정'이라는 딱지를 당당히 뗄 수 있게 되었다. 그리고 마침내 3도와 6도는 완전협화음정인 1, 4, 5, 8도에 대응하는 불완전협화음정이라는 이름을 갖게 되었다. 이 불완전협화음정과 완전협화음정이 함께 어우러진 가장 단순한 화음이 바로 아래 보이는 C 장3화음(major triad)이다. 제1음인 C음과 제2음인 E음과는 장3도, E음과 제3음인 G음과는 단 3도, 그리고 근음과 제3음 사이는 완전 5도로 구성되어 있다.
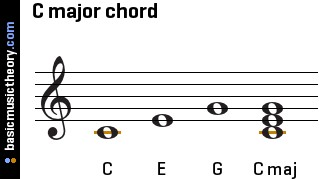
불완전협화음정으로 확립된 3도 화음이 음악 세계 전면에 나서면서 선법 체계는 거의 자취를 감추고 조성 체계가 새로이 그 자리를 차지했는데 조성 체계 하의 음악의 가장 중요한 감상 포인트 중 하나는 그 음악에 사용된 음계 및 화성 중에서 가장 기본이 되는 음과 화음을 인식하는 것이었다. 이를 각각 으뜸음(tonic) 및 으뜸화음(tonic chord)라고 부르는데, 으뜸화음은 으뜸음을 근음(根音, root)으로 하여 음계를 구성하는 음을 기준으로 3도씩 쌓아올린 화음이다. 이때 3도를 2번 쌓으면 3화음(triad), 3번 쌓으면 7화음(seventh chord)라고 부르는데, 첫 3도가 장3도이냐 단3도이냐에 따라 음악의 조성이 기쁜 음악이냐 슬픈 음악이냐가 결정되었다. 이런 이유로 으뜸화음의 첫 3도가 메이저 3도인 경우는 조성이 메이저, 즉 장조(長調)가 되며, 이 메이저 조성을 가진 다이어토닉 스케일이 곧 메이저 스케일(major scale) 혹은 장음계가 되는 것이다. 반대로 으뜸화음의 첫 3도가 마이너 3도인 경우에는 조성이 마이너, 즉 단조(短調)가 되며, 이 마이너 조성을 가진 다이어토닉 스케일이 곧 마이너 스케일(minor scale) 혹은 단음계 가 되는 것이다. 장조, 단조의 이름이 그렇게 붙은 이유는 문자 그대로 뭐 조성이 길고 짧아서 혹은 기쁜 것은 긴 감정이고 슬픈 것은 짧은 감정이라서 그런 것이 아니라 다 이런 배경이 있었던 것이다.5
한편 순정률 체계 하에서 모든 음정 간격들의 협화 및 불협화 정도는 피타고라스 음률에서와 마찬가지로 간단한 정수의 진동수 비율로 판가름되었고, 그 결과 아래와 같이 정의될 수 있었다.
| 음정 간격 | 진동수 비율 | 어울림 여부 |
|---|---|---|
| 제주 | 1:1 | 완전협화음정 |
| 옥타브 | 1:2 | 완전협화음정 |
| 완전5도 | 2:3 | 완전협화음정 |
| 완전4도 | 3:4 | 완전협화음정 |
| 장3도 | 4:5 | 불완전협화음정 |
| 단3도 | 5:6 | 불완전협화음정 |
| 장6도 | 3:5 | 불완전협화음정 |
| 단6도 | 5:8 | 불완전협화음정 |
| 장2도 | 8:9 | 불협화음정 |
| 단2도 | 15:16 | 불협화음정 |
| 장7도 | 8:15 | 불협화음정 |
| 단7도 | 9:16 | 불협화음정 |
그런데 문제는 순정률도 완벽하지 않다는 것이었고, 피타고라스 음률에서 드러난 문제 ― 딴이름한소리 문제라든지 돌고 돌아도 한 옥타브가 깔끔하게 나오지 않는다든지 ― 가 여전히 존재했다. 게다가 조성 음악 체계가 발전하면서 순정률의 또다른, 더 큰 문제점이 드러나기 시작했다.
조성에는 장조와 단조밖에 없지만, 그 장조와 단조는 으뜸음 개수를 따라 각각 12개씩 있다. 따라서 곡을 작곡할 때 같은 가락이라고 하더라도 조가 달라지면 느낌이 확연히 달라지는 것을 느낄 수 있다. 같은 가락 진행과 음정 간격을 동일하게 유지한 채 음계를 평행하게 옮기는 것을 조옮김(transposition) 혹은 이조(移調)라고 하는데, 조옮김은 대중 가요에서도 빈번하게 찾아볼 수 있다. 특히 처음 진행하던 조가 클라이맥스 부분부터 바뀌어 마지막까지 새로운 조로 진행하는 경우가 대다수이다. 아래 곡은 처음엔 E♭ 장조로 시작하지만 브릿지 이후에는 E 장조로 조옮김된다. 똑같은 '나를 믿어주길 바래~'지만 느낌이 확연히 다르다.6
또한 조바꿈(modulation) 혹은 전조(轉調)라는 것도 있다. 조바꿈은 곡의 진행 도중 조성이 바뀌는 것을 의미하지만 조옮김처럼 완전한 같은 가락과 화성 진행을 평행하게 옮기는 것은 아니며 곡의 분위기를 바꾸기 위해 도입되며 대개 다른 조로 조옮김을 하기 전에 사용되거나 아니면 다시 원래 조로 돌아가기 전에 도입되기도 한다. 같은 가수의 아래 곡은 비록 장음계와 단음계의 구분이 불명확하지만 어찌 되었든 조바꿈이 다양하게 진행되어 색다른 느낌이 느껴진다.
조성 음악이 체계를 잡아가면서 총 24개의 장단조의 성격을 구별짓고 여기에 감정을 부여하는 시도가 많이 이뤄졌다. 예를 들면 독일의 시인이자 작곡가, 오르가니스트였던 크리스티안 슈바르트(Christian Schubart)는 C 장조는 '완벽히 순수하며 단순한 아이들의 대화같은 느낌'이라고 정의한 반면 A 장조는 '흠결 없는 사랑, 애정으로 충만한 만족감'으로 그 성격을 표현했고, F 단조는 '깊은 우울함, 통곡과 절망의 울부짖음' 등으로 설명했다. 초기의 곡들은 이런 감정을 충실히 표현하기 위해 대개 하나의 조성이 처음부터 끝까지 이어지는 것들이었을 것이다. 그런데 조성 음악의 발전에 따라 사람들은 더욱 다양한 감정의 변화를 곡 안에 표현시킬 수 있는 저력을 갖추길 원했고, 이에 따라 한 곡에서의 조성을 하나에만 국한시키지 않거 점차 다양한 조옮김과 조바꿈을 통해 다양한 조성을 한 곡 안에 녹여낼 수 있게 하려고 했다. 피아노 학원에서 늘 연주하는 피아노 소나타 연습곡만 해도 이런 조옮김과 조바꿈이 수시로 등장하는 것을 알 수 있다. 예를 들어 가장 유명한 소나타 연습곡 중 하나인 볼프강 모차르트(Wolfgang Mozart)의 K.545 1악장을 들어보면 조성이 엄청 복잡하게 수시로 바뀌는 것을 알 수 있다.
우리는 앞서 순정률이 피타고라스 음률을 개선하여 장조와 단조를 확립하는 데 큰 기여를 했다는 것을 알아 보았다. 그런데 순정률 덕에 태동하게 된 조성 음악이 오히려 순정률 때문에 발전에 난항을 겪는 사태가 발생하였으니, 순정률 하에서는 바로 앞에서 언급한 조옮김과 조바꿈이 자유롭지 못하다는 것이 가장 큰 문제였다.
예를 들어 C 장조로 시작한 곡이 있었다. 이것을 그대로 E 장조로 조옮김을 했다고 가정해 보자. 그렇다면 C 장조에서의 완전 5도 관계에 있는 C음과 G음은 E 장조에서 E음과 B음으로 옮겨질 것이다. 그렇다면 진동수 비율은? C 장조에서 C음과 G음의 진동수 비율은 2:3이다. 그런데 순정률 상태에서 E음은 C음에 대해 진동수가 5/4배였고, B음은 C음에 대해 진동수가 15/8배였다. 따라서 E 장조로 조옮김 되었을 때 E음과 B음의 진동수 비율은 2:3 이 되며 이 간격은 완전 5도가 맞다. 따라서 C 장조에서 E 장조로 조옮김 하는 경우에는 가장 기본적인 협화음정인 완전5도의 울림에 큰 문제가 없다.
이번에는 D 장조로 조옮김을 했다고 가정해 보자. 그렇다면 C 장조에서의 완전 5도 관계에 있는 C음과 G음은 D 장조에서 D음과 A음으로 옮겨질 것이다. 자, 진동수 비율은? C 장조에서 C음과 G음의 진동수 비율은 2:3이다. 그런데 순정률 상태에서 D음은 C음에 대해 진동수가 9/8배였고, A음은 C음에 대해 진동수가 5/3배였다. 따라서 D 장조로 조옮김 되었을 때 D음과 A음의 진동수 비율은 27:40 이 되며 이 간격은 2:3보다 약간 작게 된다. 그 말은 무슨 말인가? C 장조에서는 맑고 곱게 들리던 완전 5도의 울림이 D 장조로 조옮김 했더니 어울리지 않는 탁한 음정이 되었다는 뜻이다. 이렇듯 순정률 하에서는 어떤 조의 경우 문제 없이 조옮김과 조바꿈을 할 수 있지만, 어떤 조의 경우에는 불가능 했다. 즉, 조옮김과 조바꿈이 자유롭지 않았다. 물론 피타고라스 음률에서도 동일한 문제가 있지만 당시에는 선법 체계였기 때문에 이런 문제가 크게 대두되지 않았다.
순정률 하에서 이런 문제를 해결하는 방법이 두 가지가 있었다.
- 연주 도중 조성이 바뀔때마다 조율을 새로 한다. 그런데 이것은 현실적인 해결책이 아니었다. 음악이 뚝 끊기는 것도 그렇거니와 조율이 순식간에 이뤄지는 것도 아니니 이런 대책은 이론적으로는 해결 가능하지만 절대 현실적이지 않은 방법이다.
- 연주자가 임의로 연주 방식을 약간 바꾼다. 예를 들어 현악기 연주자는 조옮김을 하면 현을 조금 더 짧게 짚든지 해서 협화음정이 되도록 임의로 조절한다. 관악기 연주자도 미세한 운지법 조절을 통해 음높이를 일부러 낮추거나 높여서 협화음정이 되도록 조절한다. 실제로 아주 뛰어난 연주자들은 이와 같은 방식의 연주법을 통해 다른 악기들과의 협연 중 불협화음의 발생을 최소화하기도 한다.
그런데 몇몇 악기들은 위에서 언급한 행동들 자체가 불가능했다. 예를 들어 실로폰(xylophone)의 경우 딱히 조율법이라는 게 없다. 왜냐하면 규격대로 만들어지 금속 막대기로 구성된 악기이기 때문에. 그래서 실로폰의 음높이를 조절하려면 금속을 이어붙이거나 깎아야겠지만, 어느 실로폰 연주자도 이런 무시무시한 짓을 벌이지 못할 것이다. 건반 악기들도 마찬가지였다. 건반악기들은 이미 연주 전에 조율이 된 상태로 무대에 설치되므로 도중에 조율이 불가능하거니와 연주 방법이라고 해 봐야 건반을 누르는 타건(打鍵) 뿐이므로 뭐 방법을 달리해서 음높이를 조절할 가능성도 없었다. 결국 피아노를 위시한 건반 악기들이 서양 기악 역사 전면에 등장하기 시작한 때부터 순정률의 지위는 위협을 받기 시작했다.
이 문제를 해결하기 위해 중전음률(meantone temperament)이라는 새로운 조율법이 등장했다. 본편에서는 이를 자세히 다루지는 않겠지만, 중전음률은 순정률에서 생겨나는 문제를 보정하기 위해 합리적인 꼼수(?)를 쓴 것이라고 봐도 무방하다. 그러나 중전음률도 완벽하지는 않아서 여전히 순정률이 가지던 문제가 존재했다.
작곡가들의 숙원이었던 자유로운 조옮김과 조바꿈은 16세기 후반에 개발된 평균율(平均律, equal temperament)에 의해 이뤄질 수 있었다. 기록에 따르면 평균율은 중국 명(明)나라 황족이었던 주재육(朱載堉)에 의해 최초로 엄밀한 수학적 계산 결과와 함께 소개되었다고 한다.7 비록 중국 음악계에서는 이를 크게 중요한 발견으로 여기지 않았지만, 당시 명나라에서 선교 활동을 벌이던 예수회(Jesuit) 사제들이 주재육의 서적과 기록을 곧바로 서양에 소개할 정도로 서양 음악계에서는 이 발견을 매우 흥미롭게 여겼다.
평균율의 기본 핵심은 문자 그대로 모든 음정 간격을 동등하게 나눈다는 것에 있었다. 즉, 크로매틱 스케일을 만든다고 할 때, 한 옥타브 사이를 12음의 반음으로 나누되 반음 사이의 진동수 비율을 균등하게 하는 것이 평균율의 핵심었다. 그런데 이 문제를 수학적으로 표현하면 다음 방정식의 해를 찾는 것과 같았다.
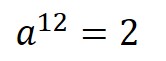
사실 평균율은 누구나가 한번쯤 생각해 볼 법한, 그리 첨단적인 아주 새로운 사상은 아니었다. 하지만 당시 사람들이 무슨 재주로 저 열두제곱근의 값을 알아낸단 말인가! 비록 많은 음악가들과 계산 잘하는 학자들이 아주 고생고생하며 어림값으로 a 값을 찾아나서긴 했지만 정확하게 들어맞지 못했고, 번번히 평균율의 도입은 실패했던 것이다. 이 문제는 17세기 초반에야 당시 수학계에 등장한 로그(logarithm)에 의해 해결될 수 있었다.


위의 방정식 양변에 상용로그를 취하면 아래와 같이 식이 바뀐다.
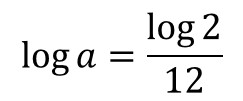
이 문제는 고등학교 수학 과정을 문제 없이 이수한 사람이라면 크게 어렵지 않게 풀 수 있는 문제이다. 계산기를 이용해도 좋지만, 수학책 뒤에 있는 상용로그표를 이용하면 a 값을 소수점 셋째 자리 이내에서 충분히 어림짐작 할 수 있을 것이다. 물론 당시 수학자들은 보다 정밀한 값을 찾으려고 소수점 셋째 자리 이하의 숫자까지 아주 필사적으로 찾아냈을 것이지만, 우리는 현대 문명의 이기가 있으니 잠시 짬을 내어 선배들의 노고 (혹은 노가다)에 경의를 표하고 바로 계산기를 두드려보자. a 값은 1.05946309435929... 와 같은 무리수로 나온다.8 결국 평균율이란 무엇이냐! 모든 반음 간격의 진동수 비율을 1:1.05946309435929... 로 고정시켜 놓은 것이라고 할 수 있겠다.
평균율 하에서는 어떤 조성이든 간에 모든 음정 간격은 동일했으므로 이때부터 조옮김과 조바꿈의 진정한 자유시대가 열렸다. 평균율 덕분에 피타고라스 음률이나 순정률에서 문제가 되었던 딴이름한소리 역시 큰 문제를 일으키지 않았고, 한 옥타브가 음정 간격에 의해 틀어지는 문제 역시 사라지게 되었다. 이 평균율에 큰 감화를 받은 한 사람이 평균율에 찬사를 보내는 작품을 만들 정도였는데 그가 바로 저 유명한 요한 제바스티안 바흐(Johann Sebastian Bach)였다.
바흐는 총 두 권의 클라비어곡집을 썼으며 각 권은 총 24개의 연습곡(?)들로 구성되어 있는데 12개의 장조 및 단조마다 서곡(prelude)와 푸가(fugue) 묶음이 있는 형태이다. 즉, 24개의 푸가 모음곡이라고 불러도 무방한 전집이다. 이 곡집에서 의미심장한 부분은 위 영상의 32분 18초의 E♭ 단조 서곡과 34분 50초의 D# 단조 푸가가 한 묶음으로 구성되어 있다는 점이다. E♭음과 D#는 평균율에서는 딴이름한소리지만, 평균율이 아닌 음률에서는 미묘하게 서로 다른 진동수를 가지는 다른 음이다. 혹시 바흐가 아무런 생각 없이 단지 실수로 표기를 잘못했던 것은 아닐까? 그런데 1시간 12분 28초부터는 A♭ 장조의 서곡과 푸가가 이어지는데 그 다음인 1시간 16분 29초부터는 G# 단조의 서곡과 푸가가 이어진다. A♭음과 G#음 역시 평균율에서만 딴이름한소리이므로 이것은 실수라고 보기에는 다분히 의도적이라고 할 수 있겠다. 따라서 다수의 학자들은 이 점을 들어 바흐가 평균율을 활용하여 클라비어곡집을 작곡했다고 여기고 있다.
이 작품의 의의는 바로 한 가지 형태로 조율된 악기를 가지고 모든 장단조의 음악을 불협화음 없이 그런대로 어울리는 듯하게 연주할 수 있다는 것이다. 순정률로 조율된 악기를 가지고 C 장조 곡을 연주하다가 D 장조 곡을 연주하면 발생하는 안 어울림의 문제 따위는 평균율에서는 없다는 것이다. 아주 대담하게 바흐는 24개 장단조 전부에 대해 멋진 곡들을 작곡하여 연주함으로써 평균율이 다른 음률에 비해 조성 체계 중심 음악에 매우 유리하다는 것을 몸소 보여주었다.
물론 기원전의 피타고라스 및 그의 학파 사람들이 살아 돌아온다면 이 평균율을 무척 저주했을 것이다. 그들의 수 체계에 포함되지 않는 더러운(?) 무리수가 조화로운 음률을 더럽혔으니(?) 말이다. 예를 들어 완전5도를 살펴보자. 피타고라스 음률 및 순정률에서 완전5도의 진동수 비율은 2:3이었다. 그러나 평균율에서는...

하지만 1.4983070768766814987992807320298 과 3/2(=1.5)의 차이는 얼마인가? 고작 0.0017 정도이다. 물론 음에 아주 예민한 사람이라면 이 정도 차이도 인식할 수 있다고 한다. 하지만 이 정도 진동수 비율이면 사람들이 쉽게 인식하기는 다소 어려운 정도라고 할 수 있다. 따라서 평균율은 화음의 어울림을 크게 해치지 않는 선에서 음정 간격을 새롭게 정의할 수 있었고, 그러면서 동시에 이전의 음률들인 피타고라스 음률, 순정률, 중전음률 등이 가지고 있던 고질적인 여러 문제들 ― 딴이름한소리 문제, 돌고 돌아 옥타브가 나오지 않는 문제 ― 을 근본적으로 해결해 주었다.
그런데 평균율에서의 진동수 비율은 옥타브를 빼고 모두 무리수이다. 따라서 화음의 어울림을 간단한 정수 진동수 비율로 정의한다면 평균율에서의 화음들은 옥타브를 빼고 전부 불협화음이 되어야 한다. 하지만, 평균율과 순정률 사이의 진동수 비율은 그렇게 큰 차이가 나지 않다고 간주될 수 있으므로 순정률 섹션에서 살펴본 음정 간격의 어울림 여부 평균율에서도 그대로 적용할 수 있다. 즉, 비록 평균율에서는 엄밀한 기준으로 따지자면, 완전5도나 장3도나 단7도나 모두 불협화음정이지만 해석의 편리와 실제 감상의 느낌에 따라 순정률에서의 고찰을 그대로 이어받아 각각 완전협화음정, 불완전협화음정, 불협화음정으로 구분지어 해석한다는 뜻이다.
앞에서 완전음정이 아닌 음정의 경우 장(長), 단(短)이 나눠지는 것을 확인했는데 (예를 들어 장3도와 단3도), 평균율에서는 장음정과 단음정 사이에는 모두 1:1.05946309435929... 진동수 비율로 정의되는 반음 차이만이 존재함을 알 수 있을 것이다. 따라서 평균율에서는 반음 간격이 훨씬 더 중요한 음정 간격 단위로 취급될 수 있다는 것 또한 알 수 있다. 참고로 한국의 중고등학교 음악 시간에 신나게 외우는 장2도, 단3도, 완전5도 등에 대한 해석 역시 모두 반음 간격의 증가 혹은 감소를 통해 이해할 수 있다.
한편 완전음정은 음정 간격이 반음씩 늘어나면 증(增, augmented)이라는 이름을 앞에 붙이고 반대로 반음씩 줄어들면 감(減, diminished)이라는 이름을 앞에 붙이는데, 평균율에서는 딴이름한소리 원칙에 따라 감4도는 장3도와 동일하고, 증5도는 단6도와 동일해진다. 그러면 완전음정도 아니고 장단음정도 아닌 음이 딱 하나 남게 된다. 바로 그것은 증4도(augmented fourth) 혹은 감5도(diminished fifth).

이 증4도의 음정 간격은 반음 6개 간격으로 나란히 붙어 있는 온음 3개 간격과 동일하다. 그런 이유로 이 음정을 따로 셋온음(tritone)이라고 부른다. 이 셋온음은 12개의 반음 간격으로 구성된 한 옥타브를 완벽하게 절반으로 나누는 것을 알 수 있다. 그리하여 증4도의 진동수 비율은 무려 1:√2 (제곱근 2)가 된다.
순정률에서 언급했지만 협화의 여부는 간단한 정수의 진동수 비율이라고 했다. 물론 평균율에서는 옥타브를 제외한 모든 음정 간격이 무리수이긴 하지만 대개 순정률의 정수비와 거의 비슷하게 근사할 수 있는 반면, 증4도는 '너무 대놓고' 무리수 비율이 된다. 사실 고대에서조차 증4도나 감5도는 굉장히 거슬리는 불협화음으로 여겨졌는데, 전편에서 다룬 피타고라스 음률에서 증4도의 진동수 비율은 512:729이고, 감5도의 진동수 비율은 729:1024였던 것을 기억해 보자. 너무나도 복잡한 숫자의 진동수 비율이다.
이런 이유로 서양 음악 발전에 지대한 공을 들인 귀도 다레초(Guido d'Arezzo)는 셋온음을 ‘Diabolus in Musica(음악의 악마)’라고 불렀고 교회 음악에서는 이 음의 사용을 자제하기 위해 선법 진행 중 가끔 B음을 B♭으로 일부러 낮추기까지 했다 (5편 참조).

이 노래로부터 오늘날 사용하는 계이름 도레미파솔라시가 나왔다고 한다.
이러한 셋온음을 피하는 전통은 고전음악 시대까지 이어졌지만, 낭만주의 시대 이후부터 풍부한 표현을 위해 점차 널리 사용되기 시작했다. 셋온음의 가장 대표적인 활용 예는 바로 카미유 생상스(Camille Saint-Saëns, 1835-1921)의 교향시인 「죽음의 무도(Danse Macabre)」이다. 12시를 알리는 하프의 종소리 연주가 끝난 뒤 갑작스럽게 등장하는 바이올린 독주자의 음은 굉장히 거슬리는 듯한 묘한 분위기를 연출하는데, 이 때 연주되는 음은 E♭'음과 A음으로 증4도 관계에 있는 음들이다. 곡 중간중간에 워낙 이 음정이 자주 등장해서 바이올린 독주자의 바이올린은 애초에 E 현이 E♭ 으로 일부러 낮게 조율된 상태이다.
그리고 한국인이라면 이 음악을 국내에서 유명하게 만든 아래 영상을 반드시 기억하고 있을 것이다.
이 외에도 증4도가 활용된 음악은 굉장히 많다. 그런데 중요한 것은 이 증4도의 출현을 단순한 새로운 음정의 활용이라는 측면에서 볼 것이 아니라 협화음정과 불협화음정에 대한 당대 음악가들의 인식 변화의 흐름에 견주어 생각해 보아야 한다는 것이다. 중세 시대의 정형화된 선법에서 벗어나 보다 인간의 감정을 풍부하게 표현할 수 있다는 조성 체계의 음악으로 진입한 서양 음악은 어느새 조성 체계조차도 버거운 멍에라고 생각을 하기 시작했고, 시대가 흐르면서 점차 증4도로 대표되는 불협화음의 금기를 깨는 행동을 서슴치 않고(!) 벌이게 되었다. 이것은 단순한 변칙적인 일탈이 아닌, 진지한 일탈이자 새로운 음악의 흐름 가운데 있었던 변혁이라고 할 수 있다. 그러다가 걸출한 서양 음악가들 중 몇몇은 조성 체계 자체를 부정하는 시도를 진행하게 되는데 5편에서 언급된 클로드 드뷔시(Claude Debussy)의 곡이 그러했고, 리하르트 바그너(Richard Wagner)의 곡들이 그러했다. 그리고 마침내 독일 출신의 작곡가 아르놀트 쇤베르크(Arnold Sch&oamult;nberg)를 필두로 한 무조성(atonality)이 20세기 초반 서양 음악을 강타했다.
과거의 시점으로 바라보면 위 음악과 같은 '현대 음악'들은 죄다 괴상망측한 불협화음으로 범벅이 된 지저분한 음악으로 간주될 것이다. 물론 그것은 오늘날 사람들의 시점에서도 마찬가지인데, 고대로부터 이어져 온 음악의 '음의 어울림'에 대한 인식이 21세기를 살고 있는 우리에게도 워낙 확고하게 심겨져 있기 때문이라고 할 수 있겠다. 하지만 피타고라스가 애써 외면하려고 했던 무리수의 세계가 유리수의 세계보다 더 넓었던 것처럼, 협화음과 조성 체계의 음악보다 불협화음과 무조성 체계의 음악이 우리를 더 넓고 다양한 세상으로 인도해 주었던 것은 확실하다.
그리고 음악의 물리학은 협화음과 불협화음을, 선법과 조성과 무조성을 구분짓거나 차별하지 않는다. 단지 그것들은 어떠한 물리학적 현상 안에 다양한 양태로서, 일종의 부분집합으로서 음악이라는 큰 집 안에 포함되어 있을 뿐이다. 그래서 우리가 물리학을 파헤쳐서 음악을 이해하는 근본적인 목표는 어쩌면 이 모든 것에 대해서 우리가 초연해지고, 차별없이 모든 것을 기쁘게 받아들일 수 있기 위해서일 지도 모르겠다.
저 유명한 물리학자 알베르트 아인슈타인(Albert Einstein)은 뛰어난 아마추어 바이올린 연주가이기도 했다. 그는 살아생전 다음과 같은 말을 했다.
If I were not a physicist, I would probably be a musician. I often think in music. I live my daydreams in music. I see my life in terms of music… I cannot tell if I would have done any creative work of importance in music, but I do know that I get most joy in life out of my violin.
내가 물리학자가 아니었다면 나는 음악가였을 것이다. 나는 음악 안에서 자주 생각하고, 음악 안에서 몽상하며, 음악적인 면에서 내 삶을 바라본다... 내가 음악 분야에서 어떤 중요한 창조적인 일을 했을는지 판단하지 못하겠지만, 내가 분명히 아는 것은 바이올린으로부터 내 인생의 기쁨 대부분을 누렸다는 것이다.

물리학과 함께 살펴본 음악 이야기가 모든 분들의 시간을 기쁘게 만들어주었기를 간절히 바라며!
- 1아이오니안 모드가 에이올리안 모드와 함께 교회 선법의 일부로 편입된 것은 16세기 스위스의 음악 이론가인 하인리히 글라레안(Heinrich Glarean)에 의해서였다.
- 2존 던스터블(John Dunstable)은 영국에서 르네상스 초기 시기에 활동한 작곡가로 3도와 6도 진행의 음악을 다수 작곡하여 당시 음악계를 신선한 충격(?)에 빠뜨린 장본인이다. 마르탱 르 프랑의 글에서도 알 수 있듯이 그의 음악은 부르고뉴 악파에 지대한 영향을 끼쳤다.
- 3이런 점에서는 일본의 음악 용어 번역이 참으로 적절했다고 생각한다. 우리는 일본의 영향을 받아서 메이저 3도를 장(長) 3도, 마이너 3도를 단(短) 3도라고 부른다. 진동수의 크고 작음을 길고 짧다는 것에 빗댄 것이다. 한편 중국에서는 직접적으로 메이저와 마이너를 번역하여 메이저 3도를 대(大) 3도, 마이너 3도를 소(小) 3도라고 부른다.
- 4그리스 문자 υ는 고대에는 '우'로 발음했지만 고전 그리스어에서는 '위'로 발음했고, 현대에는 '이'로 발음한다고 한다.
- 5참고로 독일어는 영어, 프랑스어, 이탈리아어의 장조 및 단조 표현과 완전히 다른 표현을 쓰는데, 장조를 dur라고 하고 단조를 moll이라고 한다. 샤를-루이 아농(Charles-Louis Hanon)의 연습곡에서 음계 연습편을 보면 C-dur, d-moll 이런 표기들을 볼 수 있는게 이게 각각 장조와 단조를 표현하는 단어이다. 이 명칭들은 라틴어에서 따온 것인데 dur는 durus(단단한)라는 단어에서 온 것이고, moll은 mollis(부드러운)라는 단어에서 온 것이라고 한다.
- 6물론 가수들의 목소리가 좀 더 격정적으로 변한다는 사실은 제외하고 감상하자. 어떻게 보면 조옮김을 하면 악기 소리 느낌 뿐 아니라 사람의 목소리도 느낌이 달라지니까 이것도 감상 포인트에 속하는 것일지도 모르겠다. 사람 목소리도 신체 악기 소리니까 말이다.
- 7참고로 주재육은 명나라 4대 황제인 홍희제(洪熙帝)의 6대손이라고 한다.
- 8400여년 전, 주재육이 발견한 값이 1.059463094라고 하니 굉장히 근접한 값이라고 할 수 있다.
- 9그런데 독일어로 '평균율의'에 해당하는 형용사는 gleichtemperierte이므로 바흐가 제목에 사용한 wohltemperierte와는 다르다는, 즉 바흐가 평균율을 이용한 것이 아닐 수도 있다는 의견이 음악학자들 사이에서 제기된 바가 있기는 하다.
▲[이전글] 5. 피타고라스 음률 (Pythagorean Tuning)
 |
이 저작물은 크리에이티브 커먼즈 저작자표시-비영리-동일조건변경허락 4.0 국제 라이선스에 따라 이용할 수 있습니다. |